Deep Learning básico con Keras (Parte 2): Convolutional Nets
En este segundo artículo vamos a pasar de una red neuronal sencilla a una red convolucional. Keras permite hacerlas de forma muy sencilla y básicamente, todo lo demás para medir la calidad de los modelos entrenados se hace de la misma forma.
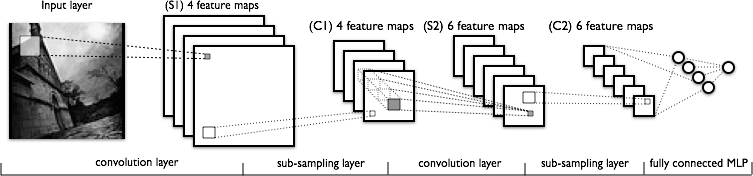
Red Convolucional
Realizaremos el mismo experimento cambiando el modelo utilizado, que pasará de ser una red neuronal "tradicional" a una red convolutiva.
Importando las librerías necesarias
De nuevo, empezamos importando las librerías. En los siguientes artículos no mostraremos esta parte, pero por ahora incidiremos en ello.
import numpy as np
from scipy import misc
from PIL import Image
import glob
import matplotlib.pyplot as plt
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline
from IPython.display import SVG
import cv2
import seaborn as sn
import pandas as pd
import pickle
from keras import layers
from keras.layers import Flatten, Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D, Dropout
from keras.models import Sequential, Model, load_model
from keras.preprocessing import image
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
from keras.applications.imagenet_utils import decode_predictions
from keras.utils import layer_utils, np_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from keras.initializers import glorot_uniform
from keras import losses
import keras.backend as K
from keras.callbacks import ModelCheckpoint
from sklearn.metrics import confusion_matrix, classification_report
import tensorflow as tf
Preparando el conjunto de datos
Como antes, usaremos el conjunto de datos CIFAR-100, que, como ya dijimos, consta de 600 imágenes por cada clase de un total de 100 clases. Se divide en 500 imágenes para entrenamiento y 100 imágenes para validación por cada clase. Las 100 clases están agrupadas en 20 superclases. Cada imagen tiene una etiqueta "fina" (la clase, de entre las 100, a la que pertenece) y una etiqueta "gruesa" (correspondiente a su superclase).
from keras.datasets import cifar100
(x_train_original, y_train_original), (x_test_original, y_test_original) = cifar100.load_data(label_mode='fine')
Actualmente, hemos descargado los datasets de entrenamiento y validación. x_train_original y x_test_original son los conjuntos de datos con lás imágenes de entrenamiento y validación respectivamente, mientras que y_train_original y y_test_original son los datasets con las etiquetas.
Veíamos que la forma de y_train_original era la siguiente:
array([[19], [29], [ 0], ..., [ 3], [ 7], [73]])
Así que, inicialmente, había que convertirlo en su versión one-hot-encoding (ver wikipedia).
y_train = np_utils.to_categorical(y_train_original, 100)
y_test = np_utils.to_categorical(y_test_original, 100)
El siguiente paso era ver los datos de entrenamiento (x_train_original)
x_train_original[0]
array([[[255, 255, 255],
[255, 255, 255],
[255, 255, 255],
...,
[195, 205, 193],
[212, 224, 204],
[182, 194, 167]],
[[255, 255, 255],
[254, 254, 254],
[254, 254, 254],
...,
[170, 176, 150],
[161, 168, 130],
[146, 154, 113]],
[[255, 255, 255],
[254, 254, 254],
[255, 255, 255],
...,
[189, 199, 169],
[166, 178, 130],
[121, 133, 87]],
...,
[[148, 185, 79],
[142, 182, 57],
[140, 179, 60],
...,
[ 30, 17, 1],
[ 65, 62, 15],
[ 76, 77, 20]],
[[122, 157, 66],
[120, 155, 58],
[126, 160, 71],
...,
[ 22, 16, 3],
[ 97, 112, 56],
[141, 161, 87]],
[[ 87, 122, 41],
[ 88, 122, 39],
[101, 134, 56],
...,
[ 34, 36, 10],
[105, 133, 59],
[138, 173, 79]]], dtype=uint8)
Representa la imagen en los 3 canales RGB de 256 píxeles. Vamos a verla.
imgplot = plt.imshow(x_train_original[3])
plt.show()

3ª imagen del dataset de entrenamiento
Lo que hacíamos a continuación, era normalizar las imágenes dividiéndo cada elemento por el numero de píxeles, es decir, 255. Con lo que obteníamos el array con valores de entre 0 y 1.
x_train = x_train_original/255
x_test = x_test_original/255
Preparando el entorno
Especificabamos la situación de los canales de las imágenes y la fase del experimento.
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
Entrenando la red convolucional
En este paso, vamos a definir el modelo de red convolucional.
def create_simple_cnn():
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), input_shape=(32, 32, 3), activation='relu'))
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(256, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(512, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(1024, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(500, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(100, activation='softmax'))
return model
Como se puede ver en el código, la instrucción Conv2D introduce una capa convolucional y la instrucción MaxPooling, la capa de pooling (en esta red hemos realizado max-pooling, pero podíamos haber usado otras como average pooling). Para cada convolución unamos como función de activación ReLu. Otra instrucción nueva es Dropout, con la que hacemos la función de regularización Dropout.
Una vez definido el modelo, lo compilamos especificando la función de optimización, la de coste o pérdida y las métricas que usaremos. En este caso, como en el anterior, usaremos la función de optimización stochactic gradient descent, la función de pérdida categorical cross entropy y, para las métricas, accuracy y mse (media de los errores cuadráticos).
scnn_model = create_simple_cnn()
scnn_model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['acc', 'mse'])
Una vez hecho esto, vamos a ver un resumen del modelo creado.
scnn_model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_7 (Conv2D) (None, 30, 30, 32) 896
_________________________________________________________________
conv2d_8 (Conv2D) (None, 28, 28, 64) 18496
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 14, 14, 64) 0
_________________________________________________________________
conv2d_9 (Conv2D) (None, 12, 12, 128) 73856
_________________________________________________________________
conv2d_10 (Conv2D) (None, 10, 10, 256) 295168
_________________________________________________________________
conv2d_11 (Conv2D) (None, 8, 8, 512) 1180160
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 4, 4, 512) 0
_________________________________________________________________
conv2d_12 (Conv2D) (None, 2, 2, 1024) 4719616
_________________________________________________________________
max_pooling2d_6 (MaxPooling2 (None, 1, 1, 1024) 0
_________________________________________________________________
flatten_2 (Flatten) (None, 1024) 0
_________________________________________________________________
dense_3 (Dense) (None, 500) 512500
_________________________________________________________________
dropout_4 (Dropout) (None, 500) 0
_________________________________________________________________
dense_4 (Dense) (None, 100) 50100
=================================================================
Total params: 6,850,792
Trainable params: 6,850,792
Non-trainable params: 0
_________________________________________________________________
Podemos ver que hemos doblado el número de parámetros. Si hubiésemos usado una red "tradicional" para lo que vamos a realizar, el número de parámetros hubiera crecido demasiado. Con el paso de la convolución, lo que va a hacer el modelo será extraer parámetros de la imagen.
Ahora sólo queda entrenar, para ello, haremos lo siguiente:
scnn = scnn_model.fit(x=x_train, y=y_train, batch_size=32, epochs=10, verbose=1, validation_data=(x_test, y_test), shuffle=True)
Le decimos a Keras que queremos usar para entrenar el dataset imágenes normalizadas de entrenamiento con el array de etiquetas one-hot-encoding. Usaremos batches o bloques de 32 (reduciendo la necesidad de memoria) y daremos 10 vueltas completas (o epochs). Usaremos los datos para validar x_test e y_test. El proceso de entrenamiento lo iremos viendo a continuación hasta terminar. El resultado del entrenamiento se guarda en la variable scnn, de la cual, extraeremos el histórico de los datos del entrenamiento.
Como se puede ver, las instrucciones tras el metodo que define el modelo son exactamente iguales.
Train on 50000 samples, validate on 10000 samples
Epoch 1/10
50000/50000 [==============================] - 59s 1ms/step - loss: 4.5980 - acc: 0.0136 - mean_squared_error: 0.0099 - val_loss: 4.5637 - val_acc: 0.0233 - val_mean_squared_error: 0.0099
Epoch 2/10
50000/50000 [==============================] - 58s 1ms/step - loss: 4.4183 - acc: 0.0302 - mean_squared_error: 0.0099 - val_loss: 4.3002 - val_acc: 0.0372 - val_mean_squared_error: 0.0098
Epoch 3/10
50000/50000 [==============================] - 58s 1ms/step - loss: 4.2146 - acc: 0.0549 - mean_squared_error: 0.0098 - val_loss: 4.1151 - val_acc: 0.0745 - val_mean_squared_error: 0.0097
Epoch 4/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.9989 - acc: 0.0889 - mean_squared_error: 0.0097 - val_loss: 3.9709 - val_acc: 0.0922 - val_mean_squared_error: 0.0096
Epoch 5/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.8207 - acc: 0.1175 - mean_squared_error: 0.0095 - val_loss: 3.8121 - val_acc: 0.1172 - val_mean_squared_error: 0.0095
Epoch 6/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.6638 - acc: 0.1444 - mean_squared_error: 0.0094 - val_loss: 3.6191 - val_acc: 0.1620 - val_mean_squared_error: 0.0093
Epoch 7/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.5202 - acc: 0.1695 - mean_squared_error: 0.0093 - val_loss: 3.5624 - val_acc: 0.1631 - val_mean_squared_error: 0.0093
Epoch 8/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.3970 - acc: 0.1940 - mean_squared_error: 0.0091 - val_loss: 3.5031 - val_acc: 0.1777 - val_mean_squared_error: 0.0092
Epoch 9/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.2684 - acc: 0.2160 - mean_squared_error: 0.0090 - val_loss: 3.3561 - val_acc: 0.2061 - val_mean_squared_error: 0.0090
Epoch 10/10
50000/50000 [==============================] - 58s 1ms/step - loss: 3.1532 - acc: 0.2383 - mean_squared_error: 0.0088 - val_loss: 3.2669 - val_acc: 0.2183 - val_mean_squared_error: 0.0089
Al igual que antes, aunque hemos evaluado durante el entrenamiento, podríamos evaluarlo frente a otro dataset.
cnn_evaluation = scnn_model.evaluate(x=x_test, y=y_test, batch_size=32, verbose=1)
cnn_evaluation
10000/10000 [==============================] - 3s 325us/step
[3.2704896587371826, 0.2177, 0.008938229732215405]
Veamos las métricas obtenidas para el entrenamiento y validación gráficamente (para ello usamos la librería matplotlib)
plt.figure(0)
plt.plot(scnn.history['acc'],'r')
plt.plot(scnn.history['val_acc'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Accuracy")
plt.title("Training Accuracy vs Validation Accuracy")
plt.legend(['train','validation'])
plt.figure(1)
plt.plot(scnn.history['loss'],'r')
plt.plot(scnn.history['val_loss'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Loss")
plt.title("Training Loss vs Validation Loss")
plt.legend(['train','validation'])
plt.show()
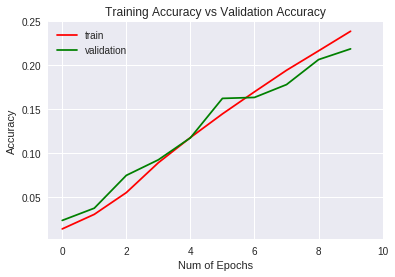
Accuracy
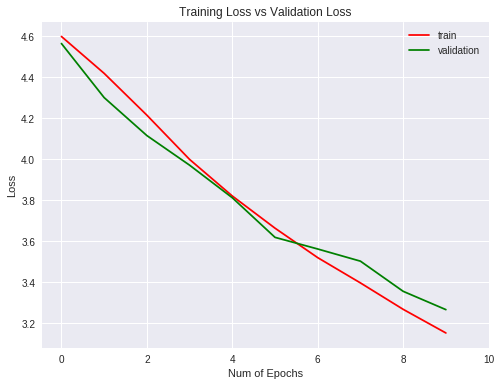
Loss
La generalización es mejor que la red sencilla ya que , a diferencia del 4% de la red sencilla, éste tiene un 2% que, ni mucho menos, es un buen resultado.
Matriz de confusión
Una vez que hemos entrenado el modelo, vamos a ver otras métricas. Para ello, crearemos la matriz de confusión con SciKit Learn y, a partir de ella, veremos las métricas precission, recall y F1-score (ver wikipedia).
Vamos a hacer una predicción sobre el dataset de validación y, a partir de ésta, generamos la matriz de confusión y mostramos las métricas mencionadas anteriormente.
scnn_pred = scnn_model.predict(x_test, batch_size=32, verbose=1)
scnn_predicted = np.argmax(scnn_pred, axis=1)
Como ya hiciéramos en la primera parte, vamos a dar como predecida el mayor valor de la predicción. Lo normal es dar un valor mínimo o bias que defina un resultado como positivo, pero en este caso, lo vamos a hacer simple.
Con la librería Scikit Learn, generamos la matriz de confusión y la dibujamos (aunque el gráfico no es muy bueno debido al numero de etiquetas).
#Creamos la matriz de confusión
scnn_cm = confusion_matrix(np.argmax(y_test, axis=1), scnn_predicted)
# Visualiamos la matriz de confusión
scnn_df_cm = pd.DataFrame(scnn_cm, range(100), range(100))
plt.figure(figsize = (20,14))
sn.set(font_scale=1.4) #for label size
sn.heatmap(scnn_df_cm, annot=True, annot_kws={"size": 12}) # font size
plt.show()

Matriz de confusión
Y por último, mostramos las métricas
scnn_report = classification_report(np.argmax(y_test, axis=1), scnn_predicted)
print(scnn_report)
precision recall f1-score support
0 0.40 0.49 0.44 100
1 0.36 0.20 0.26 100
2 0.19 0.24 0.21 100
3 0.12 0.07 0.09 100
4 0.11 0.01 0.02 100
5 0.12 0.13 0.12 100
6 0.25 0.19 0.22 100
7 0.28 0.17 0.21 100
8 0.18 0.24 0.20 100
9 0.25 0.35 0.29 100
10 0.00 0.00 0.00 100
11 0.13 0.15 0.14 100
12 0.24 0.24 0.24 100
13 0.24 0.15 0.18 100
14 0.18 0.03 0.05 100
15 0.12 0.20 0.15 100
16 0.29 0.21 0.24 100
17 0.23 0.57 0.33 100
18 0.20 0.31 0.25 100
19 0.11 0.05 0.07 100
20 0.41 0.40 0.41 100
21 0.30 0.24 0.27 100
22 0.16 0.13 0.14 100
23 0.37 0.38 0.37 100
24 0.31 0.49 0.38 100
25 0.16 0.11 0.13 100
26 0.18 0.09 0.12 100
27 0.14 0.20 0.17 100
28 0.22 0.24 0.23 100
29 0.20 0.26 0.22 100
30 0.35 0.19 0.25 100
31 0.09 0.04 0.06 100
32 0.24 0.19 0.21 100
33 0.24 0.16 0.19 100
34 0.20 0.15 0.17 100
35 0.12 0.14 0.13 100
36 0.16 0.37 0.22 100
37 0.13 0.14 0.14 100
38 0.05 0.04 0.04 100
39 0.19 0.10 0.13 100
40 0.12 0.11 0.11 100
41 0.35 0.55 0.43 100
42 0.10 0.14 0.12 100
43 0.18 0.25 0.21 100
44 0.17 0.07 0.10 100
45 0.50 0.03 0.06 100
46 0.18 0.12 0.14 100
47 0.32 0.40 0.35 100
48 0.38 0.35 0.36 100
49 0.26 0.18 0.21 100
50 0.05 0.05 0.05 100
51 0.16 0.14 0.15 100
52 0.65 0.40 0.49 100
53 0.31 0.56 0.40 100
54 0.28 0.31 0.29 100
55 0.08 0.01 0.02 100
56 0.30 0.28 0.29 100
57 0.16 0.33 0.22 100
58 0.27 0.13 0.17 100
59 0.15 0.18 0.17 100
60 0.61 0.68 0.64 100
61 0.11 0.43 0.18 100
62 0.49 0.21 0.29 100
63 0.16 0.22 0.19 100
64 0.11 0.22 0.15 100
65 0.04 0.02 0.03 100
66 0.05 0.05 0.05 100
67 0.22 0.17 0.19 100
68 0.48 0.46 0.47 100
69 0.29 0.36 0.32 100
70 0.26 0.34 0.29 100
71 0.50 0.47 0.48 100
72 0.19 0.03 0.05 100
73 0.38 0.29 0.33 100
74 0.13 0.14 0.13 100
75 0.37 0.24 0.29 100
76 0.36 0.50 0.42 100
77 0.12 0.13 0.12 100
78 0.10 0.06 0.08 100
79 0.10 0.16 0.12 100
80 0.03 0.03 0.03 100
81 0.29 0.13 0.18 100
82 0.62 0.59 0.61 100
83 0.22 0.20 0.21 100
84 0.06 0.06 0.06 100
85 0.22 0.23 0.23 100
86 0.20 0.35 0.25 100
87 0.12 0.11 0.12 100
88 0.13 0.23 0.17 100
89 0.18 0.30 0.22 100
90 0.13 0.03 0.05 100
91 0.41 0.35 0.38 100
92 0.16 0.10 0.12 100
93 0.19 0.09 0.12 100
94 0.27 0.58 0.37 100
95 0.38 0.27 0.31 100
96 0.17 0.18 0.17 100
97 0.18 0.19 0.19 100
98 0.07 0.04 0.05 100
99 0.12 0.06 0.08 100
avg / total 0.22 0.22 0.21 10000
Curva ROC (tasas de verdaderos positivos y falsos positivos)
Vamos a codificar la curva ROC para clasificación multiclase. El código está obtenido del blog de DloLogy, pero se puede obtener de la documentación de Scikit Learn.
from sklearn.datasets import make_classification
from sklearn.preprocessing import label_binarize
from scipy import interp
from itertools import cycle
n_classes = 100
from sklearn.metrics import roc_curve, auc
# Plot linewidth.
lw = 2
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], scnn_pred[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), scnn_pred.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# Compute macro-average ROC curve and ROC area
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
plt.figure(1)
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes-97), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()
# Zoom in view of the upper left corner.
plt.figure(2)
plt.xlim(0, 0.2)
plt.ylim(0.8, 1)
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(3), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()
El resultado para tres clases se muestra en los siguientes gráficos.
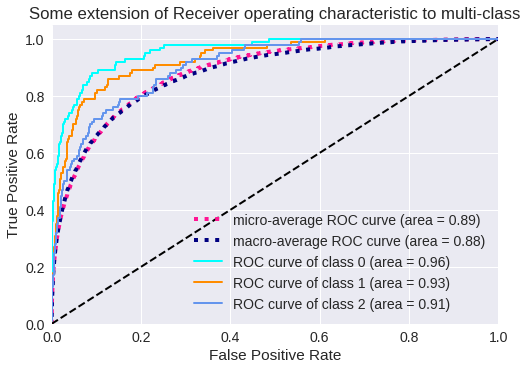
Curva ROC para 3 clases
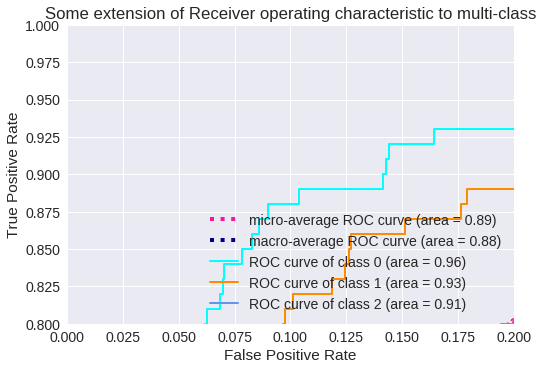
Zoom de la Curva ROC para 3 clases
Vamos a ver algunos resultados
imgplot = plt.imshow(x_train_original[0])
plt.show()
print('class for image 1: ' + str(np.argmax(y_test[0])))
print('predicted: ' + str(scnn_predicted[0]))
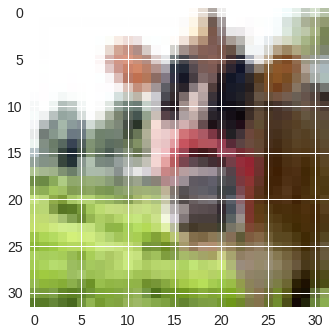
Una vaca?
class for image 1: 49
predicted: 85
imgplot = plt.imshow(x_train_original[3])
plt.show()
print('class for image 3: ' + str(np.argmax(y_test[3])))
print('predicted: ' + str(scnn_predicted[3]))

Un hombre
class for image 3: 51
predicted: 51
Salvaremos los datos del histórico de entrenamiento para compararlos con otros modelos.
#Histórico
with open(path_base + '/scnn_history.txt', 'wb') as file_pi:
pickle.dump(scnn.history, file_pi)
A continuación, vamos a comparar los datos de precisión entre el modelo entrenado con una red convolucional de este experimento con los datos del modelo anterior. Lo primero será cargar los datos del histórico del entrenamiento del modelo anterior.
with open(path_base + '/simplenn_history.txt', 'rb') as f:
snn_history = pickle.load(f)
Ya lo tenemos en la variable snn_history. Ahora, comparemos las gráficas.
plt.figure(0)
plt.plot(snn_history['val_acc'],'r')
plt.plot(scnn.history['val_acc'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Accuracy")
plt.title("Simple NN Accuracy vs simple CNN Accuracy")
plt.legend(['simple NN','CNN'])
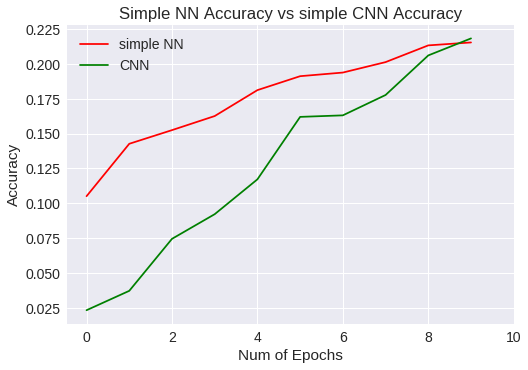
Simple NN Vs CNN accuracy
plt.figure(0)
plt.plot(snn_history['val_loss'],'r')
plt.plot(scnn.history['val_loss'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Loss")
plt.title("Simple NN Loss vs simple CNN Loss")
plt.legend(['simple NN','CNN'])
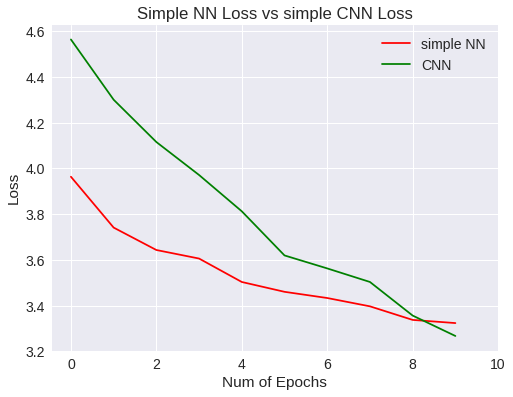
Simple NN Vs CNN loss
plt.figure(0)
plt.plot(snn_history['val_mean_squared_error'],'r')
plt.plot(scnn.history['val_mean_squared_error'],'g')
plt.xticks(np.arange(0, 11, 2.0))
plt.rcParams['figure.figsize'] = (8, 6)
plt.xlabel("Num of Epochs")
plt.ylabel("Mean Squared Error")
plt.title("Simple NN MSE vs simple CNN MSE")
plt.legend(['simple NN','CNN'])
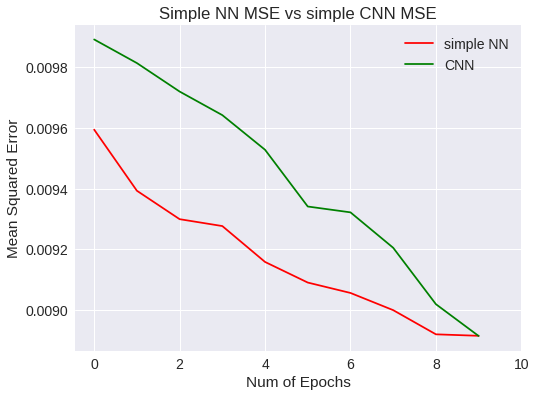
Simple NN Vs CNN MSE
Conclusión sobre el segundo experimento
A diferencia del modelo anterior, las líneas de las gráficas no toman horizontalidad, por lo que se presupone que merece la pena seguir aumentando el número de epochs para mejorar el entrenamiento. La red convolutiva ha permitido mejorar la precisión general y ha generalizado un poco mejor que la red neuronal simple.
Pero no nos dejemos engañar...
Como no es oro todo lo que reluce, hemos realizado el entrenamiento del modelo para 20 epochs más (a partir del ya entrenado). Si vemos los resultados del entrenamiento veremos lo siguiente:
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 58s 1ms/step - loss: 3.0416 - acc: 0.2552 - mean_squared_error: 0.0086 - val_loss: 3.2335 - val_acc: 0.2305 - val_mean_squared_error: 0.0089
Epoch 2/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.9324 - acc: 0.2783 - mean_squared_error: 0.0085 - val_loss: 3.1399 - val_acc: 0.2471 - val_mean_squared_error: 0.0087
Epoch 3/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.8245 - acc: 0.3031 - mean_squared_error: 0.0083 - val_loss: 3.1052 - val_acc: 0.2639 - val_mean_squared_error: 0.0086
Epoch 4/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.7177 - acc: 0.3186 - mean_squared_error: 0.0081 - val_loss: 3.0722 - val_acc: 0.2696 - val_mean_squared_error: 0.0086
Epoch 5/20
50000/50000 [==============================] - 58s 1ms/step - loss: 2.6060 - acc: 0.3416 - mean_squared_error: 0.0079 - val_loss: 2.9785 - val_acc: 0.2771 - val_mean_squared_error: 0.0084
Epoch 6/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.4995 - acc: 0.3613 - mean_squared_error: 0.0077 - val_loss: 3.0285 - val_acc: 0.2828 - val_mean_squared_error: 0.0085
Epoch 7/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.3825 - acc: 0.3873 - mean_squared_error: 0.0075 - val_loss: 3.0384 - val_acc: 0.2852 - val_mean_squared_error: 0.0085
Epoch 8/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.2569 - acc: 0.4119 - mean_squared_error: 0.0073 - val_loss: 3.1255 - val_acc: 0.2804 - val_mean_squared_error: 0.0086
Epoch 9/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.1328 - acc: 0.4352 - mean_squared_error: 0.0070 - val_loss: 3.0136 - val_acc: 0.2948 - val_mean_squared_error: 0.0084
Epoch 10/20
50000/50000 [==============================] - 59s 1ms/step - loss: 2.0036 - acc: 0.4689 - mean_squared_error: 0.0067 - val_loss: 3.0198 - val_acc: 0.2951 - val_mean_squared_error: 0.0085
Epoch 11/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.8671 - acc: 0.4922 - mean_squared_error: 0.0065 - val_loss: 3.1819 - val_acc: 0.2958 - val_mean_squared_error: 0.0086
Epoch 12/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.7304 - acc: 0.5227 - mean_squared_error: 0.0061 - val_loss: 3.2325 - val_acc: 0.3062 - val_mean_squared_error: 0.0087
Epoch 13/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.5885 - acc: 0.5527 - mean_squared_error: 0.0058 - val_loss: 3.2594 - val_acc: 0.3041 - val_mean_squared_error: 0.0087
Epoch 14/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.4592 - acc: 0.5861 - mean_squared_error: 0.0055 - val_loss: 3.3133 - val_acc: 0.2987 - val_mean_squared_error: 0.0088
Epoch 15/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.3199 - acc: 0.6170 - mean_squared_error: 0.0051 - val_loss: 3.5305 - val_acc: 0.3004 - val_mean_squared_error: 0.0090
Epoch 16/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.1907 - acc: 0.6491 - mean_squared_error: 0.0047 - val_loss: 3.6840 - val_acc: 0.3080 - val_mean_squared_error: 0.0091
Epoch 17/20
50000/50000 [==============================] - 59s 1ms/step - loss: 1.0791 - acc: 0.6787 - mean_squared_error: 0.0044 - val_loss: 3.8013 - val_acc: 0.2965 - val_mean_squared_error: 0.0093
Epoch 18/20
50000/50000 [==============================] - 59s 1ms/step - loss: 0.9594 - acc: 0.7100 - mean_squared_error: 0.0040 - val_loss: 3.8901 - val_acc: 0.2967 - val_mean_squared_error: 0.0094
Epoch 19/20
50000/50000 [==============================] - 59s 1ms/step - loss: 0.8585 - acc: 0.7362 - mean_squared_error: 0.0036 - val_loss: 4.0126 - val_acc: 0.2957 - val_mean_squared_error: 0.0095
Epoch 20/20
50000/50000 [==============================] - 59s 1ms/step - loss: 0.7647 - acc: 0.7643 - mean_squared_error: 0.0033 - val_loss: 4.3311 - val_acc: 0.2954 - val_mean_squared_error: 0.0099
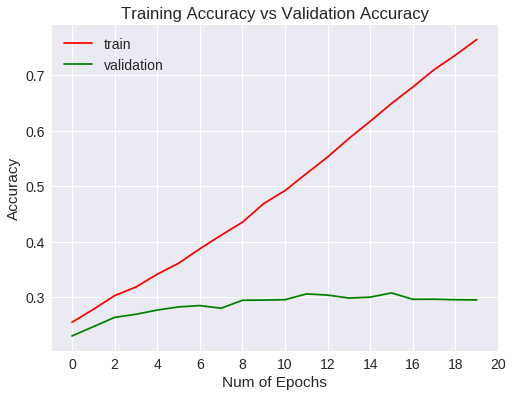
Accuracy tras 20 nuevos epochs
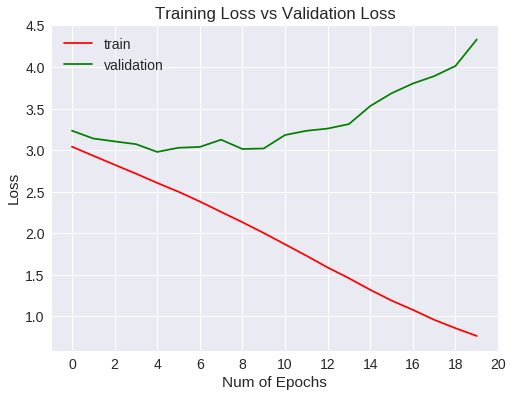
Loss tras 20 nuevos epochs
¿Qué ha pasado?
Si bién la tasa de acierto ha aumentado con respecto a los primeros 10 epochs, ocurre que a medida que aumentaba el número de entrenamientos, Empezaba a generalizar menos. Se puede ver que la función de pérdida en los datos de validación alcanza un mínimo al llegar a un valor de 3 y, a partir de ahí, va aumentando. En gráfico de accuracy indica que el algoritmo no mejora de un valor de 30%. A partir de aquí, las opciones son usar métodos para regularizar o cambiar a un modelo mejor.
En el siguiente artículo, presentaremos la primera red profunda: VGG. ¡Hasta la próxima!
 Jesús Utrera Burgal
Jesús Utrera Burgal